Через точку Р, лежащую на данной окружности, и точку Q, лежащую на данной прямой, проводится произвольная окружность, пересекающая второй раз данную окружность в точке R, данную прямую-в точке S. Доказать, что получаемые этим построением всевозможные прямые RS пересекаются в одной точке, лежащей на данной окружности.

Обозначим данную окружность через О и данную прямую через L.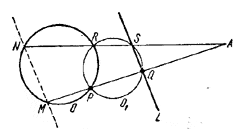

Пусть М-вторая точка пересечения прямой PQ с O. Возьмем какую-нибудь проходящую через точки Р и Q окружность О₁, которая пересекает второй раз окружность О в точке R и прямую L в точке S. Пусть N-вторая точка пересечения прямой RS с окружностью О.

Докажем, что MN || L. Для этого воспользуемся следующей известной теоремой планиметрии: если даны окружность и точка А, то для любой прямой, проходящей через А и пересекающей эту окружность в точках А₁ и А₂, произведение отрезков АА₁•АА₂ есть величина постоянная, не зависящая от выбора прямой.

Обозначим через А точку пересечения прямых PQ и RS. Сначала применим упомянутую теорему к окружности О, точке А и прямым АР и AR. Так как АР пересекает второй раз О в точке М, a AR в точке N, то

AM•AP = AN•AR. (1)

Теперь применим ту же теорему к окружности О₁, точке А и тем же прямым. Так как АР пересекает второй раз O₁ в точке Q, a AR в точке S, то

AQ•AP = AS•AR. (2)

Из (1) и (2) следует равенство

(3)

Из равенства (3) в силу теоремы, обратной теореме о пропорциональности отрезков, отсекаемых на сторонах угла параллельными прямыми, следует, что MN || QS, что и требовалось доказать.

Таким образом, для любой окружности типа О₁ точка N может быть определена как вторая точка пересечения прямой, проходящей через М и параллельной L, с окружностью О. Это построение определяет точку N однозначно независимо от выбора окружности О₁. Следовательно, всевозможные прямые RS, получаемые для различных окружностей О₁, пересекают окружность О в точке N.

Исключительные случаи, когда из (1) и (2) не следует (3), а именно когда совпадают точки R и Р или точки Q и S или когда PQ || RS, можно рассматривать как предельные для общего случая и пользоваться соображениями непрерывности.