Из точки окружности опущены перпендикуляры на стороны вписанного в нее треугольника. Доказать, что основания перпендикуляров лежат на одной прямой (прямая Симсона)

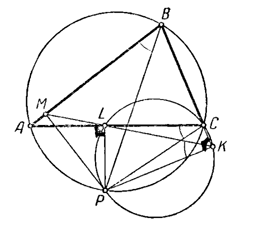
Пусть Р – точка окружности АВС и К, L, М – основания перпендикуляров, опущенных из этой точки на стороны ВС, СА и АВ треугольника. В четырехугольнике СКРL ∠PLC + ∠СКР = 180°, и потому он вписываем, откуда ∠РКL = ∠PCL. Аналогично ∠РКМ = ∠РВМ. Но ∠PCL = ∠РВМ, а следовательно, ∠РКL = ∠РКМ, и прямая KL совпадает с прямой КМ, т. е. точка К, М и N лежат на одной прямой.