Треугольник АВС после поворота около вершины А занял положение АВ’С’. Доказать, что если прямая АС делит отрезок ВВ’ пополам, то прямая АВ’ делит пополам отрезок СС’

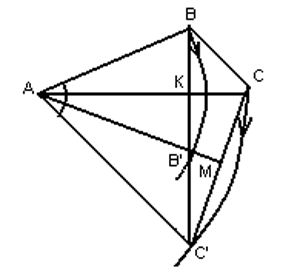
Повернем треугольник АВС вокруг вершины А на угол ВАВ’, тогда угол САС’ будет равен углу ВАВ’. По условию прямая АС делит отрезок ВВ’ пополам. Пусть К - точка деления. Треугольник АВВ’ равнобедренный, и, значит, медиана АК – также и биссектриса угла ВАВ’. Значит, углы ВАС, САВ’, В’АС’ равны, и прямая АМ, биссектриса угла САС’ равнобедренного треугольника САС’, есть его медиана, а потому отрезки СМ и МС’ равны.