В прямоугольном треугольнике АВС катеты ВС и АС продолжены за точку С так, что СА’ = СА и СВ’ = CВ. Точки А’ и В’ соединены прямой. Пусть СМ – медиана, СН – высоты треугольника АВС. Доказать, что: 1) продолжение СН’ медианы МС до пересечения с А’В’ – высота треугольника А’В’С; 2) продолжение СМ’ высоты НС до пересечения с А’В’ – медиана треугольника А’В’С.

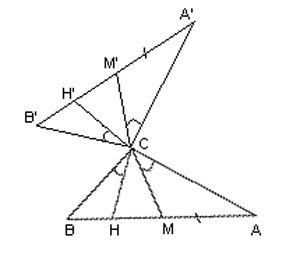
Треугольники АВС и А’В’С равны по двум катетам, а потому ∠A’ = A, B’ = B = 90° - ∠A’, при этом СМ = МА = ∠ACM = ∠A; но ∠B’CH’ = ∠ACM, как вертикальные, и, значит, ∠B’CH’ = ∠A.

Из треугольника В’СН’ находим, что СНВ’= 180° – (90° - ∠А) – ∠А = 90°, откуда следует, что СН’ – высота треугольника А’B’C.

∠М’CA’ = ∠BCH, как вертикальные, а ∠BCH = ∠А, как острые углы со взаимно перпендикулярными сторонами, и потому ∠М’CA’ = ∠А;

следовательно, равнобедренные треугольники АСМ и A’CM’ равны, а потому М’A’ = MA, т. е точка M’ в треугольнике А’В’С тоже будет серединой гипотенузы А’В’, и, следовательно, СМ’ – медиана.