В треугольнике АВС АL – биссектриса угла А.Через точку А проводят прямую перпендикулярно АL и из вершины В опускают на эту прямую перпендикуляр ВВ₁. Доказать, что периметр треугольника ВВ₁С больше периметра треугольника АВС.

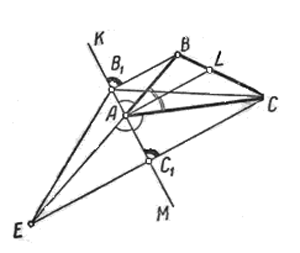
Пусть прямая КМ перпендикулярна биссектрисе АL. Опустим из точек В и С перпендикуляры ВВ₁ и СС₁ на прямую КМ и продолжим перпендикуляр СС₁ на отрезок С₁Е, равный СС₁.

Соединим прямой точку Е с точкой А и докажем, что линия ВАЕ – прямая. АL – биссектриса угла ВАС, а потому ВАВ₁ = САС₁ (1), как дополнения равных углов до прямого. Точки А и В₁ лежат на перпендикуляре МК, проведенном через середину отрезка СЕ, а потому АС = АЕ и В₁С = В₁Е (2).
Значит, треугольник САЕ – равнобедренный и его высота АС₁ есть биссектриса угла САЕ, т.е ЕАС₁ = САС₁ (3).

Из равенств (1) и (3) следует,что ВАВ₁ = ЕАС₁, но В₁АМ – прямая, следовательно, и линия ВАЕ – прямая.

В треугольнике ВВ₁Е ВА + АЕ < ВВ₁ + В₁Е, или, учитывая равенство (2), ВА + АС < ВВ₁ + В₁С; прибавив к обеим частям неравенства по ВС, получим что РАВС < РСВВ₁.