Внутри данной окружности фиксирована точка А, не совпадающая с центром. Через А проведена произвольная хорда и в ее концах - касательные к окружности, пересекающиеся в точке М. Найти геометрическое место точек М.
Пусть О - центр и R - радиус данной окружности.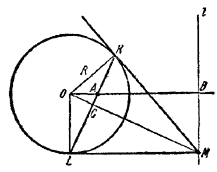
Искомым геометрическим местом является прямая l , перпендикулярная к прямой ОА и пересекающая эту прямую в точке В такой, что
![]() (1)
(1)
Доказательство. Проведем через точку М прямую l⊥ ОA, которая пересечет прямую ОА в точке В. Пусть С - точка пересечения отрезка ОМ с хордой KL. Из подобия треугольников ОАС и OMB следует:
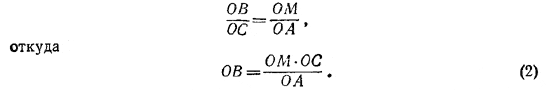
По построению КС есть высота в прямоугольном треугольнике ОКМ, следовательно,
ОМ•ОС = R2.
Подставив это выражение в (2), получим равенство (1).
Обратно, пусть М - какая-нибудь точка прямой l, перпендикулярной к ОА и такой, что ОВ определяется равенством (1). Проведем касательную МК и КС⊥OМ. Пусть КС пересечет прямую ОА в точке А'. Тогда, повторив первую часть доказательства, найдем, что ОВ определяется формулой (1) с ОА' вместо ОА. Отсюда получим ОА' = ОА, т. е. точка А' совпадет с A, а это означает, что точка М принадлежит искомому геометрическому месту.