Даны окружность К и ее хорда АВ. Рассматриваются все треугольники, вписанные в окружность и имеющие основанием данную хорду. В каждом треугольнике взята точка пересечения высот. Найти геометрическое место этих точек.

Искомым геометрическим местом является окружность, симметричная с данной окружностью К относительно данной хорды АВ.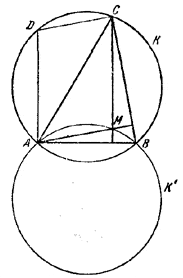

Доказательство. Построим в окружности К хорду AD⊥ AB. Пусть \(\Delta\)ABC вписан в К и М - точка пересечения его высот. Легко видеть, что AMCD - параллелограмм: DA|| СМ как перпендикуляры к АВ, a DC || AM как перпендикуляры к ВС (DC⊥BC, так как BD - диаметр в К). Поэтому точка М лежит на окружности К', получаемой из окружности К сдвигом на расстояние AD в направлении хорды DA. Ясно, что эта окружность K' симметрична с К относительно АВ.

Обратно, пусть М-точка на К' и МС⊥АВ. Так как MC = AD, то AMCD - параллелограмм и, значит, АМ || DC. Но DC ⊥ ВС, так как ABCD вписан в К и угол BAD прямой. Поэтому AM ⊥ ВС и М-точка пересечения высот в \(\Delta\)ABC. Следовательно, М принадлежит искомому геометрическому месту.