К окружности проведены две касательные. Доказать, что длина перпендикуляра, опущенного из произвольной точки окружности на хорду, соединяющую точки касания, есть среднее пропорциональное между длинами перпендикуляров, опущенных из той же точки на касательные.
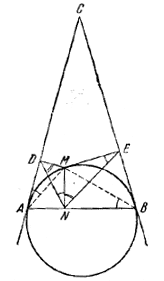
Пусть А и В — точки касания, M — произвольная точка окружности и MN ⊥ AB, MD ⊥ AC, ME ⊥ ВС.
Докажем, что треугольники DMN и NME подобны. Для этого заметим, что вокруг четырехугольников ADMN и NMEB можно описать окружности, так как
∠MNA + ∠ADМ = π/2 + π/2 = π
и
∠MEB + ∠BNM = π/2 + π/2 = π
Поэтому ∠MND = ∠MAD и ∠MEN = ∠MBN. Ho ∠MAD = ∠MBN, так как каждый из них измеряется половиной дуги AM. Итак, ∠MND = ∠MEN. Аналогично устанавливается равенство ∠NDM = ∠ENM.
Из подобия треугольников DMN и NME получаем
\(\frac{DM}{MN} = \frac{MN}{ME}\)
что и требовалось доказать.
Похожие примеры: