Доказать, что если в произвольном четырехугольнике ABCD пронести внутренние биссектрисы, то четыре точки пересечения биссектрис углов А и С с биссектрисами углов В и D лежат на окружности.

Пусть АР, BQ, CR и DS — биссектрисы внутренних углов четырехугольника ABCD.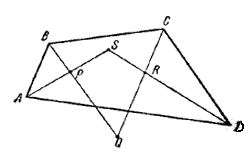

Пусть А, В, С, D — величины этих углов. Тогда

∠ ASD = π — ¹/₂ A — ¹/₂ D,

∠ BQC = π — ¹/₂ B — ¹/₂C.

Сложив эти равенства, получим:

∠ASD + ∠BQC = 2π — ¹/₂ (A + B + C + D) = 2π — ¹/₂ 2π = π.

Следовательно, точки Р, Q, R, S лежат на одной окружности.