Доказать, что во всяком треугольнике большей стороне соответствует меньшая биссектриса.
Пусть а, b, с — длины сторон треугольника, лежащих соответственно против углов А, В, С. Докажем, что длина lA биссектрисы угла А выражается формулой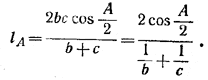 (1)
(1)
Действительно, площадь треугольника ABC равна
![]()
Отсюда следует формула (1). Аналогично для биссектрисы lB угла В получим формулу
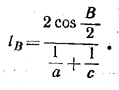 (2)
(2)
Пусть а > b; тогда ∠А > ∠В, и так как, кроме того, 0 < A/2< π/2 и 0 < B/2< π/2, то cos A/2< cos B/2
Итак, числитель дроби (1) меньше числителя дроби (2).
Далее, знаменатель 1/b + 1/c дроби (1) больше знаменателя 1/a + 1/c дроби (2), так как 1/b > 1/a.
Следовательно, lA< lB.
Похожие примеры: