Доказать, что в любом треугольнике ABC расстояние от центра описанного круга до стороны треугольника BC вдвое меньше расстояния от точки пересечения высот до вершины А.

Пусть О — точка пересечения высот, О — центр описанной окружности, Е и F — середины сторон ВС и АС.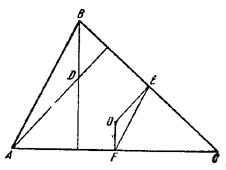

Треугольники ADB и EOF подобны, так как ∠ABD = ∠OFE и ∠BAD = ∠OEF (как углы с параллельными сторонами). Следовательно,