Определить площадь треугольника, если даны а и b— длины его сторон и t — длина биссектрисы угла между этими сторонами.

Задача сводится к определению ∠ACB =2α (рис.).

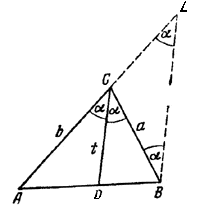
Продолжив АС и проведя BL || DC, докажем (как в теореме о биссектрисе внутреннего угла треугольника),что CL = BC= а, и из подобия треугольников ADC и ABL получаем а из равнобедренного треугольники BCL имеем BL = 2a cos α.

Следовательно, отсюда находим cos α; затем находим sin α и

S = ¹/₂ at sin α + ¹/₂ bt sin α = ¹/₂ t (a + b)sin α.

Другое решение. Площадь ¹/₂ аb sin 2α треугольника АВС есть сумма площадей ¹/₂ bt sin α и ¹/₂ at sin α треугольников ADC и BСD Следовательно,

ab sin α cos α = ¹/₂ bt sin α + ¹/₂ at sin α.

Отсюда находим cos α.