Внутри угла 60° расположена точка на расстояниях а и bот его сторон. Найти расстояние этой точки до вершины данного угла.

Продолжим ВМ (рис.) до пересечения со стороной ОА угла АОВ в точке R.

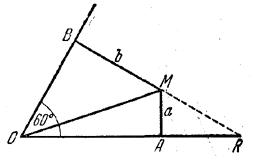
Из треугольника AMR, где∠AMR= ∠AOB = 60° (как углы с взаимно перпендикулярными сторонами), находим MR=2AM = 2a. Следовательно, RB = RM+MB =2a + b, Теперь из треугольника ROB, где OR=2OB, находим (2ОВ)² -ОВ²=(2a + b)². Следовательно,

Искомое расстояние ОМ определяется из треугольника ОВМ.

Ответ: ОМ = ²/_√3 √a² + ab + b²