Ромб с острым углом αи стороной а разделен прямыми, исходящими из вершины этого острого угла, на три равновеликие части. Определить длины отрезков этих прямых.

По условию площадь треугольника ABF (рис.) составляет ¹/₃ площади ромба ABCD, т. е. площади ²/₃ треугольника ABC.

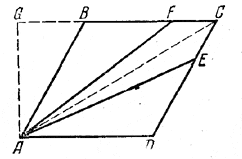
Так как треугольники ABC и ABF имеют общую высоту AG, то

BF = ²/₃BC = ²/₃a.

Поэтому

AF² = AB² + BF²- 2AВ • BF cos (180°- α) = a² + ⁴/₉ a² + ⁴/₃ a² cos α.

Ответ: AF = АЕ = ^a/₃√13 + 12 cos α.