Из точки, взятой на ребре правильной треугольной призмы со стороной основания а, проведены две плоскости. Одна проходит через сторону нижнего основания призмы под углом α к последнему, а другая — через параллельную ей сторону верхнего основания под углом β к нему. Определить объем призмы и сумму площадей полученных сечений.
Имеем (рис.) ![]() и H = BB1= BD + DB1.
и H = BB1= BD + DB1.
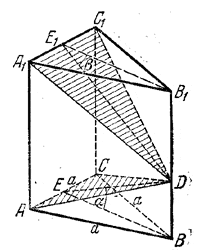
Из треугольников BED и B1E1D (Е и Е1-середины АС и A1C1) имеем
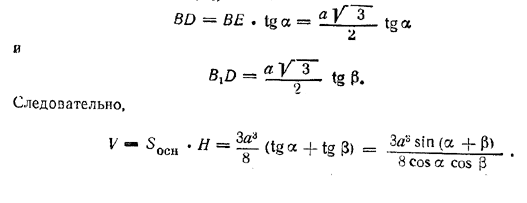
Сечение ADC проектируется на плоскость нижнего основания треугольником ABC. По доказанному (см. предварительное замечание) площадь S сечения ADC и площадь треугольника ABC, т.е. Socн.
связаны соотношением Socн.
= S cos α, так что ![]()
Таким же образом (проектируя сечение A1DC1 на верхнее основание), найдем, что площадь S’ сечения A1DC1 равна ![]()
Следовательно,
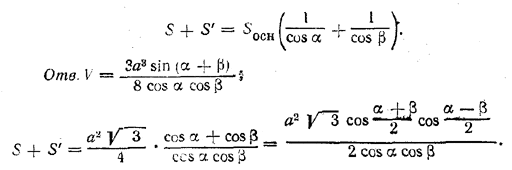
Похожие примеры: