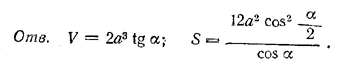В правильной четырехугольной усеченной пирамиде стороны верхнего и нижнего оснований равны соответственно а и 3а и боковые грани наклонены к плоскости нижнего основания под углом α. Через сторону верхнего основания проведена плоскость параллельно противоположной боковой грани. Определить объем четырехугольной призмы, отсеченной от данной усеченной пирамиды, и полную поверхность остальной части ее.
В сечении получится трапеция MA1B1N (рис.), равная боковой грани DD1C1C (доказать!).
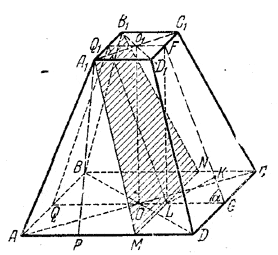
В отсеченной части A1B1C1D1MNCD имеем A1D1 = B1C1 = NC = MD, как отрезки параллельных между параллельными плоскостями. Полученное тело есть наклонная призма с основанием CC1D1D. Через апофему FG усеченной пирамиды и апофему OG основания проведем плоскость FGQQ1 : получим ∠FGL = α (доказать!). Перпендикуляр LK, опущенный из L на прямую GF, будет высотой призмы (доказать!). Из треугольника LKG, где LG = Q1F = а , имеем LK= a sin α.
Из треугольника FLG находим 
Объем призмы V вычислим по формуле
Найдем полную поверхность S тела AMA1B1NB, отсеченного плоскостью A1B1NM, Грань AA1B1B равновелика сечению MA1B1N (доказать!). Каждая из этих граней имеет площадь 
где QQ1 = FG = a/cos α . Каждая из граней АА1М и BNB1 имеет площадь 
, где AM=AD - MD = 3а - а = 2а
и A1P = FG = a/cos α. Площадь S3 грани ABNM равна S3 =AM • АВ = 2а • 3а. Имеем
S=2S1+2S2+S3.
