Сторона правильного треугольника равна а. Из центра его радиусом а/3 описана окружность. Определить площадь части треугольника, лежащей вне этой окружности.
Искомая площадь S (заштрихованная на рис.) равна утроенной площади фигуры EMFB.
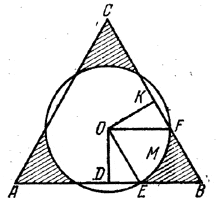
По условию OE = 1/3AB = a/3 .
B прямоугольном треугольнике OED катет OD (радиус вписанного круга) равен a√3/6; следовательно, OD = OE √3/2. Значит, ∠DEO=60°.
Точно так же ∠KFO = 60° Так как угол EBF тоже равен 60°, то EO || BF и OF || BE, и четырехугольник OEBF есть ромб со стороной a/3 и с углом 60° при вершине О.
Вычитаем площадь сектора EOF, равную 1/6 π ( a/3)2 , из площади ромба ( a/3)2 √3/2 , и pазность утраиваем.
![]()
Похожие примеры: