Зная углы треугольника, определить угол между медианой и высотой, проведенными из вершины какого-нибудь угла.

В треугольнике ABC (рис.) СЕ - высота и СО - медиана.

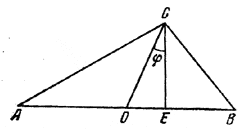
Обозначим искомый угол ОСЕ через φ, а углы треугольнику через А, В и С. Найдем из треугольников АСЕ, ВСЕ и ОСЕ cледующие выражения для отрезков основания:

AE = EC • ctgA,

BE = EC • ctg B ,

OE = EC • tg φ

Tак как AО = OB, то

АЕ - ВЕ= (АО + ОЕ) - (ОВ-ОЕ) =2ОE.

Подставив найденные выражения этих отрезков, получим

EC • ctg A - EC • ctg B = 2 EC • tg φ,

или

ctg A - ctg B = 2 tg φ.

Ответ: tg φ = ¹/₂ (ctg A - ctg В).