В равнобедренном треугольнике длины боковых сторон равны а каждая, а длина отрезка прямой, проведенного из вершины треугольника к его основанию и делящего угол между равными сторонами в отношении 1:2, равна t. Определить площадь этого треугольника.

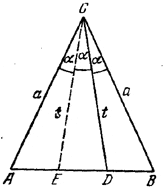
Пусть лучи CD, СЕ (рис.) делят угол АСВ на три равные части:
∠BCD = ∠DCE = ∠ECA = α. По условию АС = СВ= а и CE=CD = t.

Из треугольника ВСЕ находим, как в предыдущей задаче, затем находим sin α.

Искомая площадь есть сумма площадей треугольников АСЕ; DCE; BCD.