В ромб со стороной а и острым углом 60° вписана окружность. Определить площадь прямоугольника, вершины которого лежат в точках касания окружности со сторонами ромба.

Прямая LN, соединяющая точки касания двух параллельных прямых АВ и CD (рис.), есть диаметр окружности.

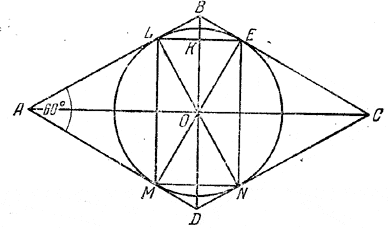
Поэтому вписанные углы LEN и LMN (и аналогично углы MLE и MNE) - прямые. Следовательно, четырехугольник LENM действительно явится прямоугольником. Треугольник ABD - равносторонний (ибо AB=AD и ∠A= 60°); отрезок LN (высота ромба) равен высоте треугольника ABD, т. е. LN = ^a√3/₂ .

Площадь S прямоугольника равна

¹/₂LN² • sin ∠LOE = ¹/₂LN² • sin ∠BAD

(стороны углов LOE и BAD взаимно перпендикулярны).

Следовательно, S = ¹/₂( ^a√3/₂)² sin 60°.