В основании пирамиды лежит прямоугольник. Одна из боковых граней имеет вид равнобедренного треугольника и перпендикулярна к основанию; в другой грани, противоположной первой, боковые ребра, равные b, образуют между собой угол 2α и наклонены к первой грани под углом α. Определить объем пирамиды и угол между указанными двумя гранями.

Высоту EF (рис.) проводим в середину F стороны DC. Соединяем вершину Е с серединой М стороны АВ. Тогда φ = ∠ FEM есть изображение угла между гранями ABE и DCE (доказать!).

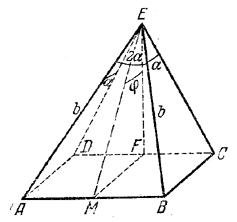
Решение. Треугольник ВСЕ - прямоугольный, и в нем ∠ BEC = α (доказать!). Значит ВС = b sin α. Из треугольника ABE имеем AB = 2b sin α и ME = b cos α. Из треугольника MFE, где MF = BC= b sin α, находим

FE = √ME²-MF² = b √cos²α - sin²α = b √cos2α .

Замечание. Подкоренное выражение cos 2α здесь всегда положительно, так как 2α<90°. Действительно, сумма двух плоских углов трехгранного угла при вершине В больше третьего ( ∠ ABС = 90°), т. е. , так что 2α<90°.

Угол φ лучше всего найти по его синусу.

Ответ: V = b³ sin²α √cos2α ; φ = arc sin (tg α).