В основании пирамиды лежит прямоугольник. Одна из боковых граней наклонена к основанию под углом β= 90°— α, а противоположная ей грань перпендикулярна к основанию и имеет вид прямоугольного треугольника с прямым углом при вершине пирамиды и острым углом, равным α. Сумма высот этих двух граней равна m. Определить объем пирамиды и сумму площадей двух других боковых граней.
Высота EF пирамиды (рис.) лежит в грани CED, перпендикулярной к плоскости основания.
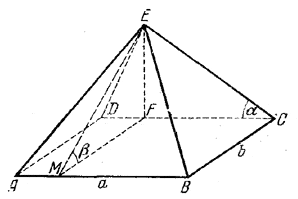
Плоскость, проведенная через EF перпендикулярно к ребру АВ, пересекает основание пирамиды по прямой MF || ВС, а боковую грань АЕВ - по прямой ME, перпендикулярной к АВ ( / EMF = β ). Прямые AD и ВС перпендикулярны к плоскости DEC, так что ∠BCE = 90° и ∠ADE=90° (все это надо доказать).
Найдем высоту H = EF. По условию EF+EM = m; кроме того,![]() . Поэтому
. Поэтому 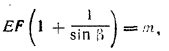 откуда
откуда
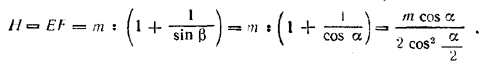
Далее из прямоугольного треугольника DEC находим
![]()
Наконец, находим
b = BC = MF = H ctg β = H tg α.
Следовательно,
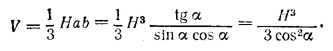
Сумма S1+S2 площадей боковых граней ВЕС и AED равна
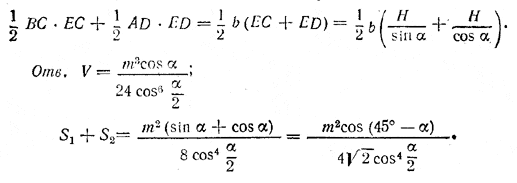
Похожие примеры: