К окружности радиуса R проведены 4 касательные, образующие ромб, большая диагональ которого равна 4R. Определить площадь каждой из фигур, ограниченных двумя касательными, проведенными из общей точки, и меньшей дугой окружности, лежащей между точками касания.
Требуется определить площадь S1 фигуры MCNF (рис.) и площадь S2 фигуры KDNE (площади фигур KALG и LBMH соответственно равны S1 и S2).
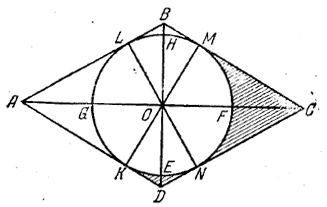
Так как по условию задачи АС = 4R, то OС = 2• OМ; следовательно, ∠OCM = 30". Значит ∠MON= 180°- 2•30°=120° и ∠KON = 60°.
Площадь четырехугольника CMON равна R2√3, а площадь сектора МОNF равна 1/3πR2. Следовательно, ![]() ; так же найдем
; так же найдем![]()
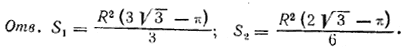
Похожие примеры: