Площадь равнобедренной трапеции, описанной около круга, равна S. Определить боковую сторону этой трапеции, если известно, что острый угол при основании трапеции равен ^π/₆.

Так как ∠A = 30° (рис.), то высота BE = h трапеции равна ¹/₂ АВ.

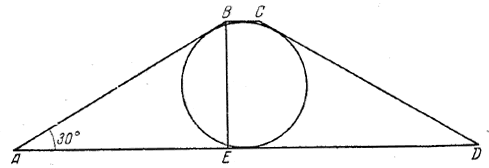
По свойству описанного четырехугольника BC + AD = AB+CD = 2AB. Поэтому

Ответ: АВ = √2S .