Через середины двух параллельных ребер куба, не лежащих на одной грани, проведена прямая, и куб повернут вокруг нее на 90°. Определить объем общей части исходного куба и повернутого, зная, что ребро куба имеет длину а.
Разрежем куб пополам диагональной плоскостью, перпендикулярной к оси вращения, и получившийся многогранник повернем на 90°. В результате возникнет изображенная на рисунке конфигурация: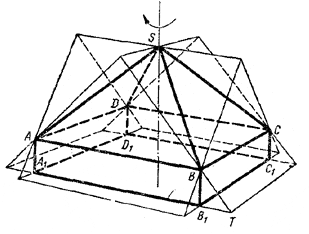
Общая часть складывается из прямоугольного параллелепипеда ABCDD1A1B1C1 и правильной пирамиды SABCD. Высоту параллелепипеда находим из \(\Delta\)ВВ1T:
![]()
Высота пирамиды
![]()
Площадь общего основания параллелепипеда и пирамиды равна a2
Таким образом, искомый объем общей части равен
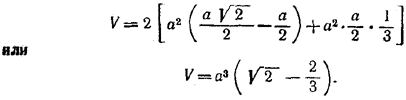
Похожие примеры: