Одна из двух треугольных пирамид с общим основанием расположена внутри другой. Доказать, что сумма плоских углов при вершине внутренней пирамиды больше, чем сумма плоских углов при вершине внешней.

Вместо того, чтобы сравнивать суммы плоских углов при вершинах S и S', сравним между собой суммы плоских углов боковых граней обеих пирамид при каждой из трех вершин общего основания. Докажем, что каждая такая сумма углов внешней пирамиды больше соответствующей суммы углов внутренней.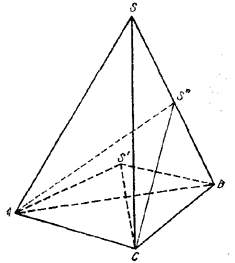

Докажем, например, что (рис.)

∠ACS + ∠SCB > ∠ACS' + ∠S'CB. (1)

Из неравенства (1) и ему аналогичных (при вершинах А и В) мы получим решение задачи. Действительно, сложив все три указанных неравенства, мы установим, что сумма Σ всех шести плоских углов боковых граней при основании внешней пирамиды больше соответствующей суммы Σ' для внутренней пирамиды:

Σ > Σ' ; (2)

Но интересующие нас в задаче величины дополняют Σ и Σ' до 540° (= 180°•3) и, следовательно, для них имеет место неравенство противоположного смысла. Таким образом, остается доказать справедливость (1).

Продолжим плоскость ACS' до пересечения с внешней пирамидой. Рассматривая трехгранный угол CS'S"B, заключаем, что

∠S'CS" + ∠S"СВ > ∠S'CB. (3)

Прибавив к обеим частям неравенства ∠ACS', получим:

∠ACS" + ∠S"CB > ∠ACS' + ∠S'CB. (4)

Но для трехгранного угла CASS" имеем:

∠ACS + ∠SCS" > ∠ACS". (5)

Заменив в неравенстве (4) ∠ACS" большей величиной, согласно (5), получим:

∠ACS + ( ∠SCS" + ∠S"CB) > ∠ACS' + ∠S'CB,

т. е. неравенство (1).