Определить площадь круга, вписанного в прямоугольный треугольник, если высота, опущенная на гипотенузу, делит ее на отрезки, равные 25,6 см и 14,4 см.

Для определения радиуса ОК = r (рис.) вписанного круга воспользуемся формулой площади треугольника S = pr (p - полупериметр треугольника).

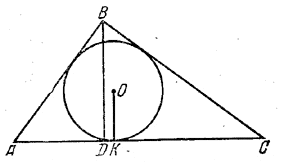
По условию AD =14,4 см, DC = 25,6 см, поэтому AС = 40 см.

Значит, АВ = √AD • АС = 24 (см), ВС = √DC • АС = 32 (см).

Следовательно, р = 48 см и S = 384 см².

Ответ: Площадь круга равна 64π см².