В круге радиуса R по одну сторону от центра проведены три параллельные между собой хорды, соответственно равные сторонам правильных вписанных в круг шестиугольника, четырехугольника и треугольника. Определить отношение площади той части круга, которая заключена между второй и третьей хордами, к площади той части круга, которая заключена между первой и второй хордами.
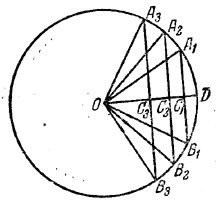
По условию (рис.) A1B1 = a6 = R, А2В2 = а4 = R√2 и А3В3 = а3 = R√3 . Высоты треугольников OA1B1 , ОА2В2 и ОА3В3 соответственно равны
OC1= R√3/2 , OC2 = R√2/2 , OC3 = R/2
Отсюда определим площади этих треугольников. Затем найдем площадь сектора OA1DB1 он составляет 1/6 площади круга; поэтому
SOA1DB1 = 1/6πR2
Аналогично SOA2DB2 = 1/4πR2 и SOA3DB3 = 1/3πR2.
Вычитая из площади каждого сектора площадь соответствующего треугольника, находим площади сегментов:
S1 = R2 ( π/6 - √3/4 ) ,
S2 = R2 ( π/4 - 1/2 ) ,
S3 = R2 ( π/3 - √3/4 ) ,
Площадь части круга, заключенной между хордами А1В1 и А2В2, равна
![]()
площадь круга, заключенная между А2В2 и А3В3, равна
![]()
Ответ: Отношение площадей равно 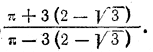
Похожие примеры: