Через одну и ту же точку окружности проведены две хорды, равные а и b. Если соединить их концы, то получится треугольник площади S. Определить радиус окружности.
Так как S = 1/2 ab sinC, где С - угол между хордами, то задача не имеет решения при S > 1/2 ab. Если S < 1/2 ab, то находим sin С = 2S/ab и существует два треугольника, имеющих стороны а и b и площадь S; у одного угол С - острый, а у другого - тупой.
В первом случае ![]() ,
,
во втором ![]()
Следовательно,
с2 = а2 + b2 - 2аb cos С = а2 + b2 + 2 √а2 b2 - 4S2
(верхний знак, если угол С острый, нижний - если тупой). При S = 1/2 ab получаем прямоугольный треугольной, так что с2 = а2 + b2 .
Радиус окружности, в которую вписан треугольник, находится по формуле
![]()
Ответ: 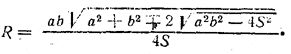
При S > 1/2 ab решений нет, при S < 1/2 ab - два решения (верхний знак, если угол между хордами острый, нижний - если тупой). При S = 1/2 ab - одно решение (хорды взаимно перпендикулярны).
Похожие примеры: