В прямом параллелепипеде стороны основания равны а и b и острый угол — α. Большая диагональ основания равна меньшей диагонали параллелепипеда. Найти объем параллелепипеда.
В отличие от прямоугольного параллелепипеда, все грани которого - прямоугольники, в прямом параллелепипеде в основании находится параллелограмм, а прямоугольниками являются только четыре боковые грани. Но при изображении прямоугольного параллелепипеда мы вынуждены изображать основание также в виде параллелограмма.. Поэтому чертеж прямого параллелепипеда по существу ничем не отличается от чертежа прямоугольного параллелепипеда, и это создает дополнительные трудности при пользовании чертежом: необходимо помнить, что острый угол параллелограмма на чертеже является острым и в самом деле у изображенной фигуры. Для большей ясности рекомендуется на чертеже делать этот угол очень острым, как на рис., и обязательно отмечать его буквой (в данном случае - буквой α).
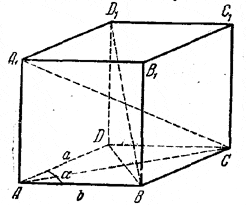
Решение. В прямом параллелепипеде диагонали (всего их четыре) попарно равны: А1С=АС1 и ВD1 = В1D (на рис. АС1 и DB1 не проведены). Пусть острый угол основания ABCD есть ∠DAB = α ; тогда ∠ABC = 180°- α тупой, и AC > BD.
Значит, меньшая диагональ параллелепипеда есть BD1 (ибо BD12 = H2 + BD2, тогда как А1С2 = Н2 + АС2; следовательно, BD12 < A1C2).
Из условия ВD1 = АС можно найти H. Именно, из треугольника BDD1 имеем
H2 = BD12 - BD2 = AC2 - BD2.
Из треугольника ABD находим
BD2 = a2 + b2 -2ab cos α,
а из треугольника ABC находим
АС2 = a2 + b2 -2ab cos (180°- α).
Следовательно, H2 = 4ab cos α.
Ответ: V = 2 sin α √(ab)3 cos α