Диагонали прямого параллелепипеда равны 9 см и √33 см. Периметр его основания равен 18 см. Боковое ребро равно 4 см. Определить полную поверхность и объем параллелепипеда.

Обозначим бoльшую сторону основания (АВ на рис.) через а, меньшую (ВС) - через b.

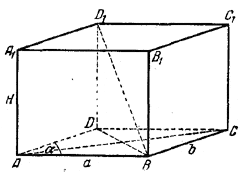
По условию а + b = 9 (см). Чтобы найти а , b, а также острый угол α, вычислим диагонали основания.

Как доказано в решении предыдущей задачи, меньшая диагональ [ BD₁ = √33 (см) ] параллелепипеда проектируется на плоскость основания диагональю BD. Поэтому

ВD² = BD₁² - DD₁² = (√33)² - 4² = 17 (см²).

Точно так же найдем AС² = 65 (см²). Получаем два уравнения

a² + b² -2ab cos α =17; a² + b² + 2ab cos α = 65.

Складывая их, находим a² + b² = 41, что вместе с а + b = 9 дает а = 5, b = 4 (мы обозначили через а большую сторону).

Вычитая, находим 4ab cos α = 48, т. е.

Следовательно,

S_ocн. = ab sin α = 4•5•0,8=16 см².

Ответ: V = 64 см³ , S_п. = 104 см²