Найти высоту тетраэдра, объем которого равен V. Под тетраэдром здесь понимается правильный четырехгранник (иногда тетраэдром называется произвольная треугольная пирамида).
Основание можно изобразить любым треугольником ABC. Центр основания изображается точкой О пересечения медиан. (Затем две из этих медиан, как не имеющие значения для решения задачи, можно стереть, оставив только точку О на медиане АЕ).
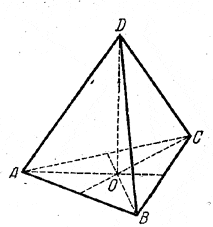
Решение. Имеем V = 1/3 • Socн. • Н = 1/3 • 1/4 a2 √3H . Связь между а и Н найдем из треугольника AOD, где AD = a, а АО есть радиус R, круга, описанного около основания, так что a = R√3.
Имеем ![]()
Подставляя a2 = 3/2 H2 в выражение V, получаем V = √3/8 H3.
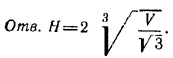
Похожие примеры: