Найти объем и боковую поверхность правильной шестиугольной пирамиды, если даны боковое ребро l и диаметр d круга, вписанного в основание пирамиды.
Соединив середины М и N (рис.) сторон ВС и FE, получаем изображение MN диаметра вписанного круга, так что MN = d и ОМ = d/2 .
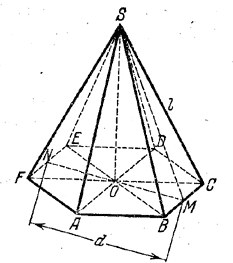
Так как ОМ есть высота равностороннего треугольника со стороной a ( = ВС = ОС = OB), то d/2 = a√3/2 , откуда а = d/√3.
Высоту H = OS находим из треугольника SCO:
![]()
Апофему m = SM пирамиды находим из треугольника SCM:
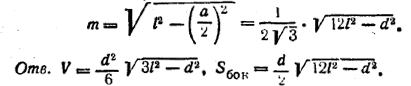
Похожие примеры: