Две окружности радиусов R и r находятся в положении внешнего касания. К этим окружностям проведена общая внешняя касательная, и в образовавшийся при этом криволинейный треугольник вписана окружность. Найти ее радиус.
Обозначим радиус искомой окружности через х. Проведем через ее центр О3 (рис.) прямую MN || AB.
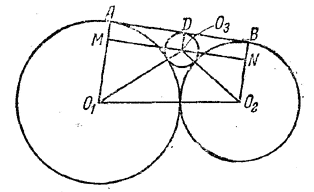
Так как прямая АВ перпендикулярна к радиусам O1A, О2В и O3D, то AM = BN = x и, значит, O1M = R- х и O2N = r - х. Кроме того, имеем O1O3 = R + x и O2O3 = r + x. Следовательно,
МО3 = √(R + x)2 - (R - x)2 = 2√Rx ,
точно так же
NO3 = 2√rx .
А так как MN = 2 √Rr (см. задачу 317), то
2√Rx + 2√rx = 2√Rr,
откуда
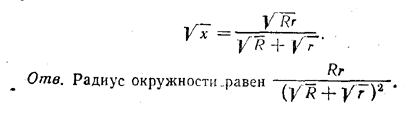
Похожие примеры: