К двум окружностям радиусов R и r, находящимся в положении внешнего касания, проведены их общие касательные - внутренняя и две внешние. Определить длину отрезка внутренней касательной, заключенного между внешними касательными.

Через точку M проходят две касательные (MD и MA)' к окружности О₁. Значит, MD = MA.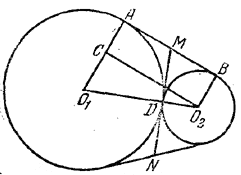

Так же докажем, что MD = MB. Следовательно,

MN = 2MD = AM + MB = AB.

Чтобы найти AB, проведем прямую О₂С, параллельную AB. Из треугольника O₁O₂C, где О₂С = AB, О₁О₂ = R + r и O₁C = R - r, получаем

AB = √(R + r)² - (R - r)²

или

AB = 2√Rr

Отв. MN = 2√Rr