К двум окружностям радиусов R и r, находящимся в положении внешнего касания, проведены их общие внешние касательные. Определить площадь трапеции, ограниченной этими касательными и хордами, соединяющими точки касания.

Пусть MN - общая касательная к двум окружностям.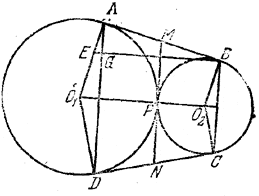


Так как AM = MP = MB, то MN - средняя линия трапеции ABCD.

Имеем MN = AB = 2√Rr (см. решение предыдущей задачи). Найдем теперь высоту BG трапеции. По теореме о пропорциональных линиях в прямоугольном треугольнике (EAB) имеем

Но

BE = О1О2 = R + r

Следовательно,





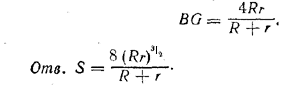
Похожие примеры:
Основанием пирамиды служит равнобедренная трапеция, в которой параллельные стороны равны а и b ( а > b), а неравные отрезки диагоналей образуют угол φ. Найти объем пирамиды, зная, что высота пирамиды, опущенная из вершины, проходит через точку пересечения диагоналей основания, а двугранные углы, прилежащие к параллельным сторонам основания, относятся как 2:1.  Смотреть решение→
Два шара касаются между собой и граней двугранного угла, величина которого α. Пусть А в В - две точки касания этих шаров с гранями (А и В принадлежат разным шарам и разным граням). В каком отношении отрезок АВ делится точками пересечения с поверхностями этих шаров? Смотреть решение→
По основаниям а и b и боковым сторонам с и d трапеции определить ее диагонали m и n.  Смотреть решение→