Основанием пирамиды служит равнобедренная трапеция, в которой параллельные стороны равны а и b ( а > b), а неравные отрезки диагоналей образуют угол φ. Найти объем пирамиды, зная, что высота пирамиды, опущенная из вершины, проходит через точку пересечения диагоналей основания, а двугранные углы, прилежащие к параллельным сторонам основания, относятся как 2:1.

Пусть AD = a, BC = b.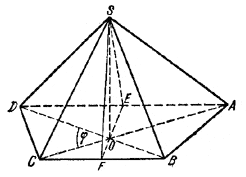

Проведем отрезок EF, соединяющий середины оснований трапеции. Очевидно, что двугранный угол, прилегающий к AD, меньше угла, прилежащего к ВС.

Пусть ∠SEO = α, тогда ∠SFO = 2α.

Имеем;

SO = OF • tg 2α = OE • tg α.

Но

OF = ^b/₂ tg ^φ/₂; OE = ^a/₂ tg ^φ/₂

и мы приходим к уравнению a tgα = btg 2α, решив которое, найдем:

*) Этот результат показывает, что в случае a < 2b задача теряет смысл.

Далее, получаем:

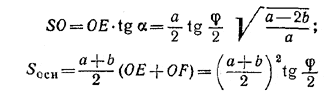
и, наконец, объем пирамиды равен