Стороны треугольника: а = 13, b = 14, с = 15. Две из них (а и b) служат касательными к кругу, центр которого лежит на третьей стороне. Определить радиус круга.

По условию а = ВС = 13 см, b = СА = 14см, с = АВ = 15 см.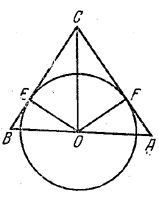

Обозначим OE = OF через R. Площадь треугольника ABC равна сумме площадей треугольников ВОС и АОС. Так как площади этих треугольников равны соответственно ^13R/₂ и ^14R/₂ то

S_ABC = ^27R/₂

С другой стороны, по формуле Герона

S_ABC= √21 (21 - 15) (21 - 14) (21 - 13) = 84 cм².

Приравниваем друг другу эти выражения площади.

Отв. R = 6 ²/₉см.