Основание треугольника делится высотою на части в 36 см и 14 см. Перпендикулярно к основанию проведена прямая, делящая площадь данного треугольника пополам. На какие части эта прямая разбила основание треугольника?

По условию AD= 36 см и DС = 14 см.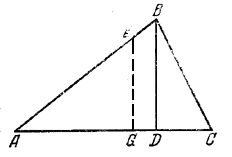

Площади S₁ и S₂ треугольников ADB и СВD, имеющих общую высоту, относятся как основания, т. е.

S₁ : S₂ = 36 : 14 = ¹⁸/₇.

Следовательно, S₁= ¹⁸/₂₅ S, гдеS = S₁ + S₂ есть площадь треугольника ABC. По условию прямая EG делит пополам площадь S; значит, эта прямая пересечет основание АС между точками А и D (а не между D и С). Получим треугольник AGE; его площадь S₃ равна ¹/₂S. Так как площади подобных треугольников AGE и ADB относятся как квадраты сторон AG и AD, то

¹⁸/₂₅ S : ¹/₂S = 36² : AG².

Отсюда найдем

AG = 30 (см).

Значит,

GC= AC-AG = (36 + 14)- 30 = 20 см.

Отв. 30 см и 20 см.