Расстояние между центрами двух окружностей, радиусы которых равны 17 см и 10 см, равно 21 cм. Определить расстояние центров от точки, в которой прямая центров пересекается с общей касательной окружностей.

Так рак расстояние между центрами окружностей меньше суммы, но больше разности их радиусов, то окружности пересекаются; значит, они имеют общую внешнюю касательную и не имеют общей внутренней касательной. Положим O₁C = x и O₂C = у.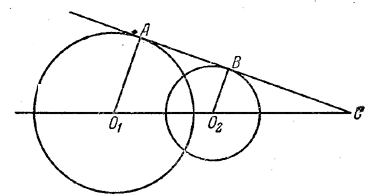

Имеем

x - y = О₁О₂ = 21 см и x : у = O₁A : O₂В= 17 : 10.

Отв. O₁C = 51 см, O₂C= 30 см.