Внешняя касательная двух окружностей радиусов 5 см и 2 см в 1¹/₂ раза больше их внутренней касательной. Определить расстояние между центрами этих окружностей.

Проведем О₂E параллельно АВ и О₂Р параллельно DC.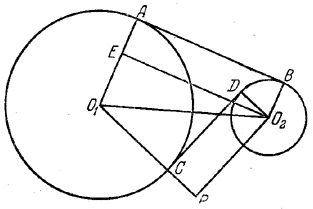

По условию АВ = ³/₂ CD. Обозначим CD через x.

Тогда О₂Р = х, О₂Е = ³/₂ х. Из треугольников O₁EO₂ и О₁РО₂ имеем

О₁О₂ ² = О₁Е² + ⁹/₄ x² и О₁О₂ ² = О₁P² + x²

Приравниваем эти два выражения и учитываем, что

О₁Е = О₁A - EA = О₁A - O₂B = 5 - 2 = 3 см

и аналогично

O₁P = O₁C + O₂D = 7 см.

Тогда получаем

9 + ⁹/₄ x²= 49 + x²,

откуда x²= 32
Поэтому

О₁О₂ ² = 49 + 32 = 81.

Отв. О₁О₂ ² = 9 см.