Стороны треугольника равны 6 см, 7 см, 9 см. Из трех вершин, как из центров, проведены взаимно касающиеся окружности, причем окружность, центр которой лежит в вершине наименьшего угла треугольника, имеет с остальными двумя окружностями внутреннее касание, а остальные две между собой имеют внешнее касание. Определить радиус трех окружностей.

По условию AB= 6 м, AС = 7 м, ВС = 9 м.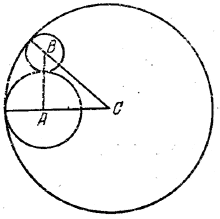

Пусть R_A, R_B и R_C - искомые радиусы окружностей с центрами в A, В и С

Тогда R_A + R_B= 6, R_C - R_A= 7, R_C - R_B = 9. Отсюда находим радиусы R_A, R_B и R_C.

Отв. R_A = 4 м, R_B = 2 м, R_C = 11 м