Три окружности радиусов r, r₁ и R касаются попарно внешним образом. Найти длину хорды, отсекаемой третьей окружностью от общей внутренней касательной первых двух окружностей.

Пусть К — точка касания двух окружностей, имеющих радиусы rи r₁ и Р —основание перпендикуляра, опущенного из центра О₂ третьей окружности на OO₁ (рис.).

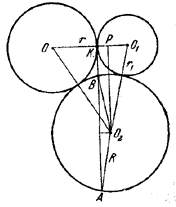
Положив КР = х, будем иметь:

AB = 2√R²— x² (1)

Величина хопределяется из уравнения

(R + r)² — (r + х)² = (R + r₁)² — (r₁ — х)²

и равна Подставив это значение в (1), получим: