На окружности даны две неподвижные точки А и В и подвижная точка M. На продолжении отрезка AM вне окружности откладывается отрезок MN=MB. Найти геометрическое место точек N.

Искомое геометрическое место состоит из двух дуг окружностей: дуги BE с центром в середине С дуги АВ данной окружности и дуги BF с центром в середине второй дуги АВ данной окружности, причем EAF-касательная в точке А к данной окружности.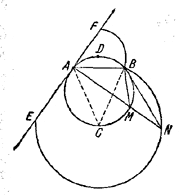

Доказательство. Пусть N - точка искомого геометрического места, полученная с помощью точки М, взятой на нижней дуге АВ. По построению \(\Delta\)NMВ равнобедренный, откуда

∠BNA =¹/₂ ∠BMA = ¹/₂ ∠ВСА.

Следовательно, точка N лежит на окружности с центром С, проходящей через точки А и В. Далее, точка N должна находиться внутри ∠ВАЕ, т. е. она лежит на дуге BE окружности с центром С. Обратно, если N лежит на этой дуге, то

∠BNA = ¹/₂ ∠ВСА= ¹/₂ ∠ВМА,

откуда следует, что ∠BNA= ∠NBM и \(\Delta\)NMB равнобедренный. Значит, точка N получается указанным построением. Аналогично проводится доказательство в случае, когда точка М будет на верхней дуге АВ.