В пространстве даны точки А, В, С и D, причем |АВ| = |ВС| = |CD|, ∠АВС = ∠BCD = ∠CDA = α. Найти угол между прямыми АС и BD.

Зафиксируем ΔABC, тогда в ΔADC известны две его стороны |AС| и |DC| и угол ∠ADC = ∠α. Построим в плоскости ΔADC окружность радиуса |АС| с центром в С (рис. а).

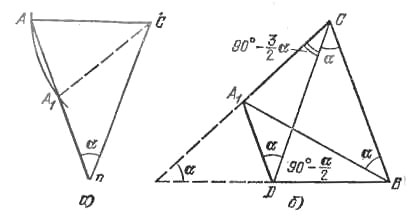
Если α ≥ 60°, то существует лишь один треугольник, имеющий данные стороны и угол (вторая точка А₁ окажется по другую сторону от точки D), это треугольник, равный треугольнику АВС. В этом случае АС и BD перпендикулярны.

Если же α < 60°, то существует вторая возможность (на рис. а это ΔА₁DC), для которой ∠СA₁D = 90° + α/2

∠A₁CD = 90° - 3α/2. Но в этом случае в вершине С (рис. б) сходятся углы BCA₁ = 90° - α/2, BCD = α, ∠A₁CD = 90° - 3α/2, а поскольку 90° - α/2 = (90° - 3α/2) + α, то точки A₁, В, С и D лежат в одной плоскости и угол между А₁С и BD будет α.

Ответ: если α ≥ 60°, то угол между АС и BD равен 90°, если α < 60°, то угол между АС и BD может быть равен или 90°, или α.