Две окружности радиусов R и r (R > r) имеют внутреннее касание. Найти радиус третьей окружности, касающейся первых двух окружностей и их общего диаметра.

Пусть О₁ , О₂ — центры соответственно окружностей радиусов R, r, а О₃—центр третьей окружности. Пусть х — радиус третьей окружности и Р — точка касания ее с диаметром О₁О₂ (рис.).

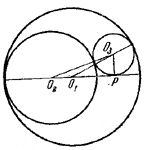
Применив теорему Пифагора к треугольникам О₂О₃Р и О₁О₃Р, получим равенство

Подставив сюда значения О₂О₃ = r+ x , О₃Р =х , О₂О₁ =R— r, О₁О₃= R— x, получим уравнение относительно неизвестного x :

(r + x)² = x²+ (R — r + √(R— x)²— x² )².

Решив это уравнение, найдем