Первое решение. Пусть ABC—данный треугольник, K₁ — вписанная окружность радиуса r и K₂ — описанная окружность радиуса R. Построим вспомогательный треугольник A₁B₁C₁так, чтобы его стороны были параллельны сторонам $\Delta$ABC и проходили через вершины $\Delta$ABC.

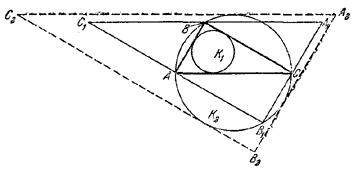
Проведем касательные к окружности K₂, параллельные сторонам $\Delta$A₁B₁C₁, руководствуясь следующим правилом: касательная А₂В₂, параллельная стороне А₁В₁, касается K₂ в точке, лежащей на той же дуге $\breve{AB}$, на которой лежит вершина С и т. д. Отрезки проведенных касательных образуют $\Delta$A₂B₂C₂.

Тогда $\Delta$A₁B₁C₁лежит внутри $\Delta$A₂B₂C₂и эти два треугольника подобны. Поэтому радиус R' окружности, вписанной в $\Delta$A₁B₁C₁, не больше радиуса R окружности K₂, вписанной в $\Delta$A₂B₂C₂, т. е. R' < R; с другой стороны, отношение радиусов окружностей, вписанных в подобные треугольники A₁B₁C₁и ABC, равно отношению сходственных сторон этих треугольников, т. е. $\frac{A_{1}B_{1}}{AB} = 2$.

Таким образом, R' = 2r. Сопоставляя это равенство с неравенством R' < R, окончательно получаем:

2r <R.

Второе решение. Пусть r, R — радиусы вписанной и описанной окружностей, S — площадь данного треугольника, р — полупериметр, а, b — стороны. Тогда

Но

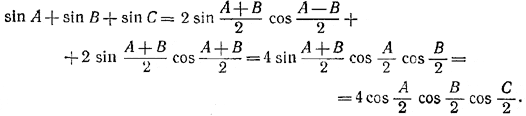
Следовательно,

Задача сводится к доказательству неравенства

Третье решение. Из формулы l² = R² — 2Rr, доказанной в предыдущей задаче, следует, что R² — 2Rr > 0, откуда R > 2r.