Доказать, что для любого прямоугольного треугольника справедливо неравенство
0,4 < r/ h < 0,5,
где r - радиус вписанного круга, h - высота, опущенная на гипотенузу.Пусть a, b — длины катетов и с — длина гипотенузы. Сравнив два выражения для площади треугольника, получаем:
S = 1/2 (a + b + c) r = 1/2 hc
откуда
![]()
Так как а + b > с, то
![]()
Далее, неравенство a2 + b2 >2ab в силу соотношения c2 = a2 + b2равносильно неравенству 2c2 > (a + b)2, или a + b < с √2. Поэтому
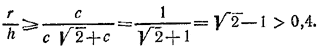
Похожие примеры: