Доказать, что в прямоугольном треугольнике сумма катетов равна сумме диаметров вписанной и описанной окружностей.

Пусть А₁, B₁, C₁ — точки касания вписанного круга со сторонами \(\Delta\)ABC, D — центр вписанного круга.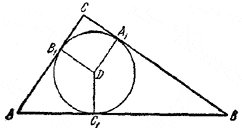

Так как отрезки касательных, проведенных из одной точки к окружности, равны, то

СА₁ = СВ₁, ВА₁ = ВС₁, АВ₁ = АС₁.

Кроме того,

DB₁ = CA₁, B₁C = A₁D.

Следовательно,

АС + ВС = СА₁ + А₁В + CB₁ + B₁A = B₁D + A₁D + BC₁ + AC₁ = 2r + 2R,

где r — радиус вписанного, а R — радиус описанного круга.