Доказать, что в прямоугольном треугольнике биссектриса прямого угла делит пополам угол между медианой и высотой, опущенными на гипотенузу.

Пусть в \(\Delta\)ABC угол ABC прямой, BD — высота, BE — биссектриса и BF — медиана.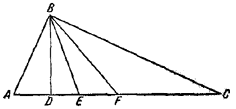

Так как BF = FC, то ∠CBF = ∠AСВ. Но

∠ABD = ^π/₂ — ∠BAD = ∠ACB.

Следовательно, ∠ABD = ∠CBP и

∠DBE = ∠ABE — ∠ABD = ∠CBE — ∠CBF = ∠FBE,

что и требовалось доказать.